|
| |
Remonter
Quelques notions (très) élémentaires... (Lien vers.. Cours d'apprentissage : L'IRM pas à pas.)
Le
corps entier du patient est soumis à un champ magnétique très puissant (1.5
Tesla à Poitiers) capable de modifier l’orientation des atomes de certaines
molécules. En imagerie, ce sont les protons (chargés électriquement +) des
atomes d’hydrogène qui sont
utilisés. Les protons d’hydrogène sont particulièrement nombreux dans le
corps humain(combinés à l’oxygène, ils forment les molécules d’eau :
H2O).
Rappelons que chez l’homme, l’eau
représente
75% du poids total. Ces protons qui possèdent des propriétés magnétiques
vont s’aligner dans la même direction que celle du champ magnétique de
l’appareil. (Alors qu’à l’état naturel, ils sont orientés dans tous les
sens).
A l’aide d’un générateur
d’ondes radiofréquences (RF), il est possible de modifier l’orientation
simultanée de ces protons. C’est le principe de la résonance magnétique
nucléaire (nucléaire, car il s’agit du noyau des atomes d’hydrogène). Après
l’arrêt de la stimulation RF de très courte durée, les protons aimantés
ont tendance à reprendre leur orientation d’origine en restituant l’énergie
sous forme d’ondes radiofréquences. Ces ondes seront amplifiées et
captées par une antenne de réception (voir rubrique : Appareillage),
analysées et reconstruites par un
puissant ordinateur sous forme d’images.
Chaque
tissu possède sa propre densité de
protons, d’où des comportements différents. Ces différences sont à
l’origine du contraste des images. Il est possible de réaliser des images en
coupe dans les trois plans de
l’espace.
Dans
certains cas, une injection d’un produit par voie intraveineuse
sera nécessaire (environ 50% des examens) pour rehausser le contraste
entre différents tissus (en pathologie inflammatoire, infectieuse ou tumorale).
Ce
produit s’appelle Gadolinium, il
n’a pratiquement aucun effet secondaire.
En savoir un peu
plus sur
le gadolinium?
Bien
que le contraste soit généralement excellent pour les tissus mous sur les
images d’IRM, il y a des circonstances ou les propriétés biophysiques
des tissus normaux et pathologiques sont semblables. En conséquence
l’utilisation d’un produit de contraste devient nécessaire. On sait depuis
1946 que le taux de relaxation nucléaire T1
de l’eau pouvait être
augmenté par l’addition d’ions paramagnétiques, tels que le nitrate
ferrique. La plupart des lanthanides et des métaux de transition sont paramagnétiques,
en raison d’un nombre impair d’électrons sur leur couche orbitale externe.
Lorsqu’ils sont dissous dans un fluide, les ions paramagnétiques agissent
comme des réhausseurs de la relaxation locale pour les protons environnants. En
conséquence, les temps de relaxation T1 et T2
diminuent tous les deux en présence
de substances paramagnétiques. A des concentrations faibles ou intermédiaires,
le raccourcissement de T1
est prédominant. De ce fait, une récupération plus complète de la
magnétisation entre les mesures se traduit par une augmentation de la force du
signal sur les images pondérées en T1.
Le Gadolinium
(Gd3+)
est l’agent, modifiant la relaxation du proton, le plus efficace de tous les
ions paramagnétiques.
Pour
utiliser les propriétés du gadolinium, il faut relier chimiquement le métal
à une molécule vectrice (ces molécules sont appelées ligands)
possédant une haute affinité pour le gadolinium. La molécule résultante est
appelée Chélate .
On
parlera donc de Chélate de gadolinium.
Quelque soit le fabricant, les doses administrées sont : 0.2 ml par Kg. A
titre d’exemple, une personne de 50 Kgs recevra une quantité de 10 ml.
|
Bases physiques de l'Imagerie
par Résonance Magnétique (IRM)
La résonance magnétique nucléaire est un
phénomène physique de découverte relativement récente décrit pour la
première fois à la fin des années 40 par Bloch et Purcell dont les travaux
furent récompensés par un prix Nobel.
Il est lié au fait que certains noyaux possèdent un très faibles moment
magnétique. Jusqu'au début des années 70, où ont été présentées les
premières images rudimentaires, la RMN est restée un outil de spectroscopie
utilisé par les physiciens, chimistes et biologistes pour étudier la structure
fine des édifices moléculaires. Les premières images par résonances
magnétique nucléaire sont apparu début des années 80 et le signal utilisé
pour la réalisation des images par résonance magnétique nucléaire résulte
des propriétés magnétiques des noyaux d'hydrogène. C'est la raison pour
laquelle lorsque nous utilisons le terme de proton, il s'agira le plus souvent
du proton en tant que noyau de l'atome d'hydrogène et non au sens plus large de
constituant des autres noyaux.
En radiologie conventionnelle ou en tomodensitométrie, le signal constituant
l'image est fonction de la densité électronique des tissus par
l'intermédiaire de leur coefficient linéaire d'absorption. En IRM, les
paramètres conditionnant le signal sont beaucoup plus nombreux et conduisant de
ce fait à une extraordinaire richesse d'informations. Citons parmi ces
paramètres :
 La densité de protons, bien sur, mais s'il
était le seul, les images obtenues ne serait pas très éloignées de celles
obtenues au scanner. La densité de protons, bien sur, mais s'il
était le seul, les images obtenues ne serait pas très éloignées de celles
obtenues au scanner.
 Les temps de relaxations longitudinal (T1) et
transversale (T2) du proton. Les temps de relaxations longitudinal (T1) et
transversale (T2) du proton.
 Les phénomènes de flux qui modifient le
signal de résonance magnétique du proton, etc ... Les phénomènes de flux qui modifient le
signal de résonance magnétique du proton, etc ...
La résonance magnétique nucléaire est un phénomène physique de découverte
relativement récente décrit pour la première fois à la fin des années 40
par Bloch et Purcell dont les travaux furent récompensés par un prix Nobel.
Il est lié au fait que certains noyaux possèdent un très faibles moment
magnétique. Jusqu'au début des années 70, où ont été présentées les
premières images rudimentaires, la RMN est restée un outil de spectroscopie
utilisé par les physiciens, chimistes et biologistes pour étudier la structure
fine des édifices moléculaires. Les premières images par résonances
magnétique nucléaire sont apparu début des années 80 et le signal utilisé
pour la réalisation des images par résonance magnétique nucléaire résulte
des propriétés magnétiques des noyaux d'hydrogène. C'est la raison pour
laquelle lorsque nous utilisons le terme de proton, il s'agira le plus souvent
du proton en tant que noyau de l'atome d'hydrogène et non au sens plus large de
constituant des autres noyaux.
En radiologie conventionnelle ou en tomodensitométrie, le signal constituant
l'image est fonction de la densité électronique des tissus par
l'intermédiaire de leur coefficient linéaire d'absorption. En IRM, les
paramètres conditionnant le signal sont beaucoup plus nombreux et conduisant de
ce fait à une extraordinaire richesse d'informations. Citons parmi ces
paramètres :
Le phénomène de RMN :
Interaction d'une radiofréquence avec le système de spins
Jusqu'à maintenant, nous ne nous sommes intéressés qu'au
comportement des spins dans un champ statique Bo. Une expérience de
RMN, qu'il s'agisse d'imagerie ou de spectroscopie, consiste à placer
les noyaux dans un champ statique Bo avec les conséquences que nous
avons décrites sur la population de spin. L'obtention du signal de
RMN se fait en modifiant l'état énergétique de la population de
spins par l'interaction avec une onde électromagnétique. C'est le
retour du système à l'état initial, à l'arrêt de l'excitation
radio fréquence (RF) qui génèrera le signal de RMN.
Une onde R.F. appliquée à la fréquence de Larmor wo = g . Bo sur un
ensemble de spin polarisés par un champ magnétique statique Bo crée
un signal de résonance dont la valeur au temps t après l'arrêt de
l'impulsion R.F. est :
S(t) = M exp(j. wo t) . exp (_t/T2*)
M est l'aimantation d'équilibre qui dépend de la fréquence
d'imagerie utilisée et des paramètres intrinsèques (r, T1, T2). T2*
est le temps de relaxation transversale apparent :
1/T2* = 1/T2 + g DBo en champ homogène DBo = 0 et par suite T2* = T2.
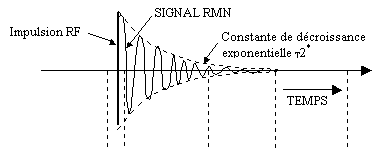
Le signal s(t) a la valeur maximum s(0) = M à l'instant t=0, c'est-à-dire
immédiatement après l'arrêt de l'impulsion R.F. Cependant des
raisons techniques, en particulier la durée d'éblouissement des
antennes et les temps de commutation des gradients, imposent un délai
d'attente entre la fin de l'impulsion R.F.et la lecture du signal.
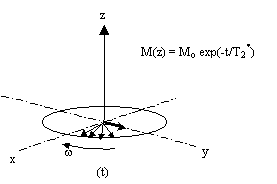
Pendant ce temps t, le déphasage entre les spins entraîne une décroissance
de signal avec la constante de temps (1/T2*).
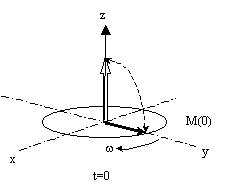
Pour faciliter la lecture du signal, on effectue la mesure après
refocalisation des spins qui est obtenue selon deux modalités : méthode
des "échos de spins" et des "échos de gradient".
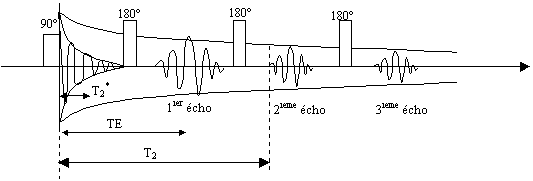
a) ECHOS DE SPINS
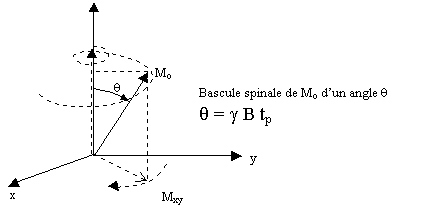
Basculement de spin.
Tp est la durée d'application de l'onde (ou impulsion) RF
excitatrice.
Dans le jargon de la RMN, on appellera "impulsion p/2" une
impulsion RF qui bascule Mo d'un angle de 90° ( c'est-à-dire qui la
couche dans le plan transverse xOy).Une impulsion P bascule Mz de 180°
etc ...
Une impulsion 180° ( fonction porte P ) appliquée à l'instant TE/2
(Temps Echo) après l'impulsion R.F. initiale (90° par exemple)
inverse l'ensemble des spins qui refocalisent à l'instant TE sous la
forme d'un écho.
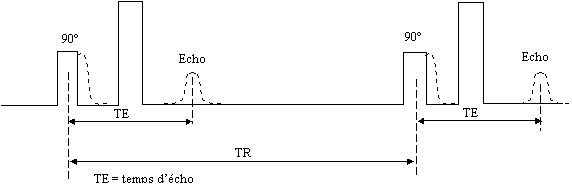
Cette méthode compense les inhomogénéités magnétiques du champ
statique et permet ainsi de limiter la décroissance du signal par
rapport à la valeur qui serait observée, au même instant TE, en
l'absence d'impulsion 180° de refocalisation. A l'instant TE
l'amplitude du signal est donc : s(t) = M exp(-TE/T2)
Les séquences d'échos de spins sont très utilisées en imagerie car
elle perment d'obtenir un bon rapport signal/bruit et compensent les
inhomogénéïtés magnétiques qui sont à l'origine d'artéfacts
dans les images. Elles présentent cependant certains inconvénients :
Le temps d'acquisition des image est relativement long car le temps d'écho
TE doit être supérieur au temps d'éblouissement desantennes, de
l'ordre de quelques dizaines de millisecondes.
Le dépôt d'énergie R.F. au patient peut être élevé pour des
impulsions 180° de forte amplitude. L'inversion du système de spins
par l'impulsion 180° ne permet pas d'obtenir l'état d'équilibre
dynamique (SSFP) requit pour la réalisation des séquences d'imagerie
rapide.
Pour palier ces inconvénients d'autres méthodes d'imagerie ont été
mises au point, dans lesquelles des gradients magnétiques remplacent
les impulsions 180° de rephasage pour assurer la refocalisation des
spin. Le signal est alors obtenu sous la forme d'un "écho de
gradient".
b) ECHOS DE GRADIENT.
Un gradient magnétique appliqué après l'impulsion R.F. initiale accélère
le déphasage entre les spins. Son inversion au temps TE/2 inverse le
sens du déphasage des spins et prodit à l'instant TE une
refocalisation du système de spins qui permet de recuellir un signal
d'écho.
Cette méthode ne permet pas cependant de compenser les inhomogénéités
du champ statique et par suite le signal observé à l'instant TE est
: s(t) = M(0) . exp(-TE/T2) qui est inférieur à celui obtenu au
moyen de la technique d'écho de spins. Elle permet cependant
d'utiliser des temps d'écho TE très courts, de l'ordre de quelques
millisecondes, d'autant plus courts que le gradient est plus intense.
Ces méthodes sont de ce fait les plus utilisées dans les techniques
d'imagerie rapides.
Image d'une distribution de densité de proton.
Imagerie IRM
GENERALITES
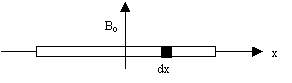
M(x) étant la densité linéique d'aimantation, l'aimantation d'un élément
d'étendue dx est M(x).dx. Une onde RF appliquée à la fréquence de
Larmor wo = g Bo, crée un signal s(t) dont la valeur à l'instant t
après l'arrêt de l'impulsion est :
dso(t) = M(x) exp (j wo t) exp (-t/T2*) dx

Le signal correspond à l'ensemble de la distribution est :
so(t) = ò M(x) exp (j wo t) exp (-t/T2*) dx
comme M(x) = 0 en dehors de la distribution on a aussi :
so(t) = ò M(x) exp (j wo t) exp (-t/T2*) dx
so(t) = M exp (j wo t) exp (-t/T2*), avec M = ò M(x) . dx
M est l'aimantation de l'ensemble de la distribution.
So(t) est un signal exponentiellement amorti, de fréquence wo, dont
l'enveloppe a pour equation : s(t) = exp (-t/T2*) ò M(x) . dx = M . exp
(-t/T2*)
Le signal obtenu correspond à la mise en résonance, avec la même fréquence
wo, de tous les spins, ce qui ne permet pas d'obtenir une image de la
distribution. Il faut pour cela connaître la contribution qu'apporte au
signal total, so(t) , l'aimantation M(x) de chaque point de la
distribution. On y parvient en réalisant un "codage en fréquence"
de l'objet au myen d'un gradient magnétique de direction Ox. Pour cela,
on superpose au champ statique Bo un champ magnétique dont l'intensité
dépend de la position, x et appelé de ce fait "gradient magnétique".

Le gradient de champ est généralement linéaire, d'intensité
constante, Gx et la valeur du champ magnétique total en un point
quelconque, x, est :Bx = Bo + x Gx
Chaque spin a donc une fréquence de résonance wx = g (Bo + xGx) qui dépend
de la position x. Par suite une onde R.F. d'étendue spectrale Dw, centrée
sur la fréquence de Larmor wo crée un signal de résonance décomposable
par transformée de Fourier (T.F.) en ses différentes composantes fréquentielles
wx, la valeur de wx dépendant directement de la position x. On peut
ainsi assigner à chaque composante spectrale wx du signal s(t) une
position x, ce qui réalise le codage en fréquence de la distribution
de spins. A chaque fréquence wx analysée dans le signal s(t)
correspond un point x de la distribution tel que : wx = g (Bo + x Gx).
Soit x = (wx/g) –Bo/ Gx
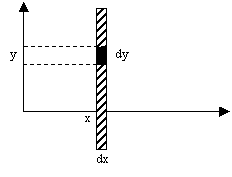
IMAGE D'UNE DISTRIBUTION PLANE
Dans le cas d'une distribution plane, le gradient Gx permet de
determiner, conformément aux développements précédents,
l'aimantation d'une rangée de spins parallèle à l'axe Oy et de
largeur dx :
[ ò M(x,y) dy ]dx
|
|
Pour différencier les
pixels selon l'axe Oy, on applique, préalablement au gradient
de lecture Gx, un gradient qui déphase les spins dont le fréquence
de résonance n'est plus wo mais :
wy = g (Bo+Gx . x + Gy . y)
Pour cette raison Gy est appelé gradient de phase et réalise
un codage en phase de l'image.
|
En pratique l'intensité du gradient Gy est ingrémentée lors de chaque
acquisition selon la relation : Gy = Go (n – (N-1)/2) avec 0< n
< (N-1)
N est le nombre de lignes choisi pour construire l'image.
Cette méthode de reconstruction d'image est la plus utilisée
actuellement. Elle consiste donc à créer un déphasage local des spins
au moyen d'un d'un gradient de phase Gy, ce qui justifie sa denomination
"spin-Warp". La détermination de l'aimantation M(x,y) en
chaque point est obtenue en effectuant une T.F. bidimentionnelle,
portant sur les variables kx (discrétisation de x) et n, du signal
mesuré S(kx,n). Cette opération est réalisée au m couleur oyen de
procédures informatiques rapides, FFT (Fast Fourier Transform) d'où le
nom de 2DFT également donné à cette méthode.
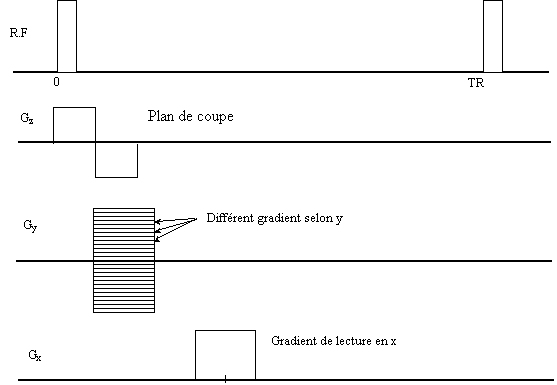
Séquence d'acquisition d'une image couleur.
Retour haut de page
|
|